Problems tagged with "least squares"
Problem #003
Tags: linear regression, least squares
Suppose a line of the form \(H(x) = w_0 + w_1 x\) is fit to a data set of points \(\{(x_i, y_i)\}\) in \(\mathbb R^2\) by minimizing the mean squared error. Let the mean squared error of this predictor with respect to this data set be \(E_1\).
Next, create a new data set by adding a single new point to the original data set with the property that the new point lies exactly on the line \(H(x) = w_0 + w_1 x\) that was fit above. Let the mean squared error of \(H\) on this new data set be \(E_2\).
Which of the following is true?
Solution
\(E_1 > E_2\)
Problem #012
Tags: least squares
Suppose a data set \(\{\nvec{x}{i}, y_i\}\) is linearly-separable.
True or false: a least squares classifier trained on this data set is guaranteed to achieve a training error of zero.
Solution
False
Problem #020
Tags: least squares
In the following, let \(\mathcal D_1\) be a set of points \((x_1, y_1), \ldots, (x_n, y_n)\) in \(\mathbb R^2\). Suppose a straight line \(H_1(x) = a_1 x + a_0\) is fit to this data set by minimizing the mean squared error, and let \(R_1\) the be mean squared error of this line.
Now create a second data set, \(\mathcal D_2\), by doubling the \(x\)-coordinate of each of the original points, but leaving the \(y\)-coordinate unchanged. That is, \(\mathcal D_2\) consists of points \((2x_1, y_1), \ldots, (2x_n, y_n)\). Suppose a straight line \(H_2(x) = b_1 x + b_0\) is fit to this data set by minimizing the mean squared error, and let \(R_2\) be the mean squared error of this line.
You may assume that all of the \(x_i\) are unique, as are all of the \(y_i\).
Part 1)
Which one of the following is true about \(R_1\) and \(R_2\)?
Solution
\(R_1 = R_2\)
Part 2)
Which one of the following is true about \(a_0\) and \(b_0\)(the intercepts)?
Solution
\(a_0 = b_0\)
Part 3)
Which one of the following is true about \(a_1\) and \(b_1\)(the slopes), assuming that the initial slope is positive?
Solution
\(a_1 > b_1\)
Problem #062
Tags: linear regression, least squares
Suppose a linear regression model \(H(\vec x) = w_0 + w_1 x_1 + w_2 x_2\) is trained by minimizing the mean squared error on the data shown below, where \(x_1\) and \(x_2\) are the features and \(y\) is the target:
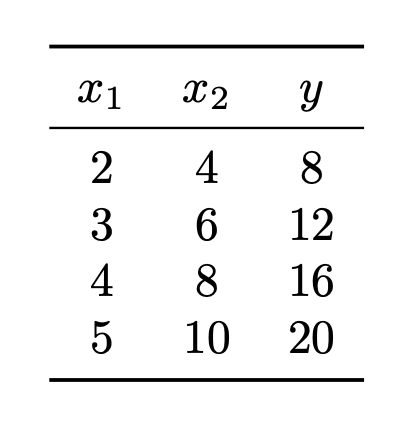
True or False: there is a unique weight vector \(\vec w = (w_0, w_1, w_2)^T\) minimizing the mean squared error for this data set.
Solution
False.
\(y\) can be predicted exactly using only \(x_1\). In particular, \(y = 4x_1\). So the weight vector \(\vec w = (0, 4, 0)^T\) is one that minimizes the mean squared error.
On the other hand, \(y\) can also be predicted exactly using only \(x_2\). In particular, \(y = 2x_2\). So the weight vector \(\vec w = (0, 0, 2)^T\) is another that minimizes the mean squared error.
In fact, there are infinitely many weight vectors that minimize the mean squared error in this case. Geometrically, this is because the data are all along a 2-dimensional line in 3-dimensional space, and by doing regression we are fitting a plane to the data. There are infinitely many planes that pass through a given line, each of them with a different corresponding weight vector, so there are infinitely many weight vectors that minimize the mean squared error.
Now you might be thinking: the mean squared error is convex, so there can be only one minimizer. It is true that the MSE is convex, but that doesn't imply that there is only one minimizer! More specifically, any local minima of a convex function is also a global minimum, but there can be many local minima. Take, for example, the function \(f(x, y) = x^2\). The point \((0, 0)\) is a minimizer, but so is \((0, 2)\) and \((0, 100)\), and so on. There are infinitely many minimizers!
Problem #080
Tags: least squares, linear prediction functions
Consider the binary classification data set shown below consisting of six points in \(\mathbb R^2\). Each point has an associated label of either +1 or -1.
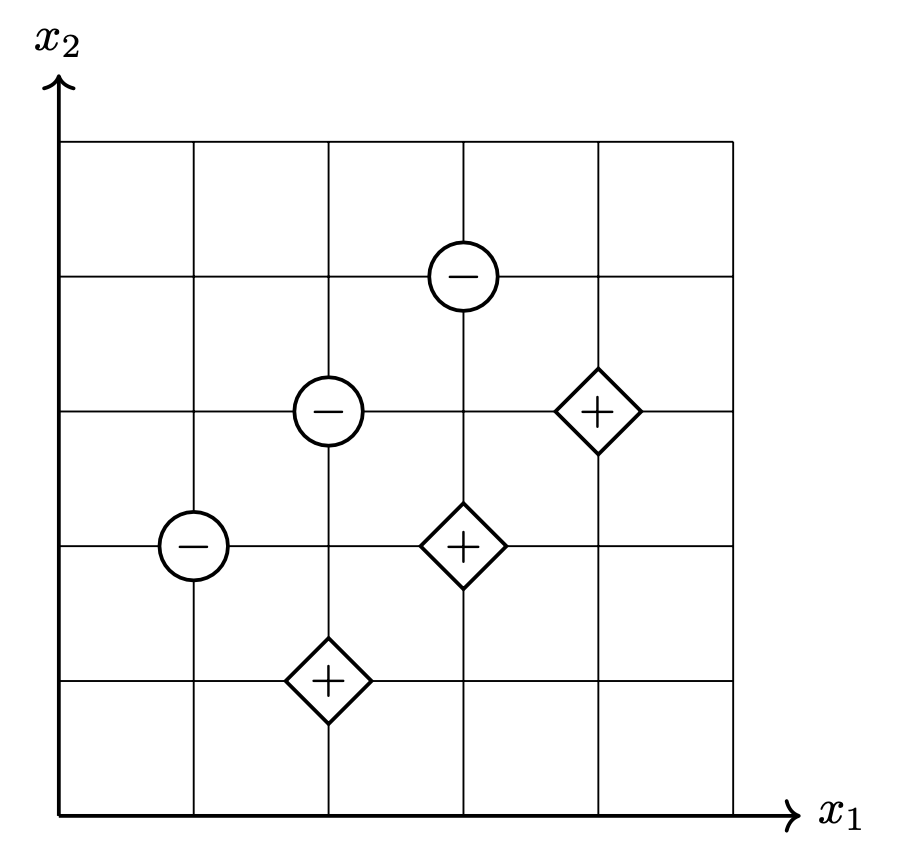
What is the mean squared error of a least squares classifier trained on this data set (without regularization)? Your answer should be a number.